2 Diagramas causales

Código

library(tidyverse)
library(lubridate)
library(kableExtra)
ggplot2::theme_set(ggplot2::theme_light())

Podemos utilizar diagramas causales introducidos por Judea Pearl (Pearl, Glymour, y Jewell (2016)) para explicar por qué el análisis se hace de manera diferente en cada uno de los casos de arriba. Los diagramas causales son representaciones de nuestro conocimiento de dominio acerca de cómo se relacionan de manera causal las variables de interés. En el caso de cálculos renales, podemos escribir el diagrama como sigue:

Código

library(dagitty)
library(ggdag)
dag_1 <- dagitty('dag{"Tratamiento" [exposure,pos="-3,0"]
  "Resultado" [outcome,pos="3,0"]
  "Tamaño" [pos="0,1"]
  "Tamaño"  -> "Tratamiento"
    "Tamaño" -> "Resultado"
    "Tratamiento" -> "Resultado"
  }')
dag_1_tidy <- tidy_dagitty(dag_1) 
dag_1_tidy |>
  ggplot(aes(x = x, y = y, xend = xend, yend = yend )) + 
  geom_dag_edges() +
  geom_dag_point(colour = "salmon", size = 20) +
  geom_dag_text(colour = "gray20") +
  theme_dag()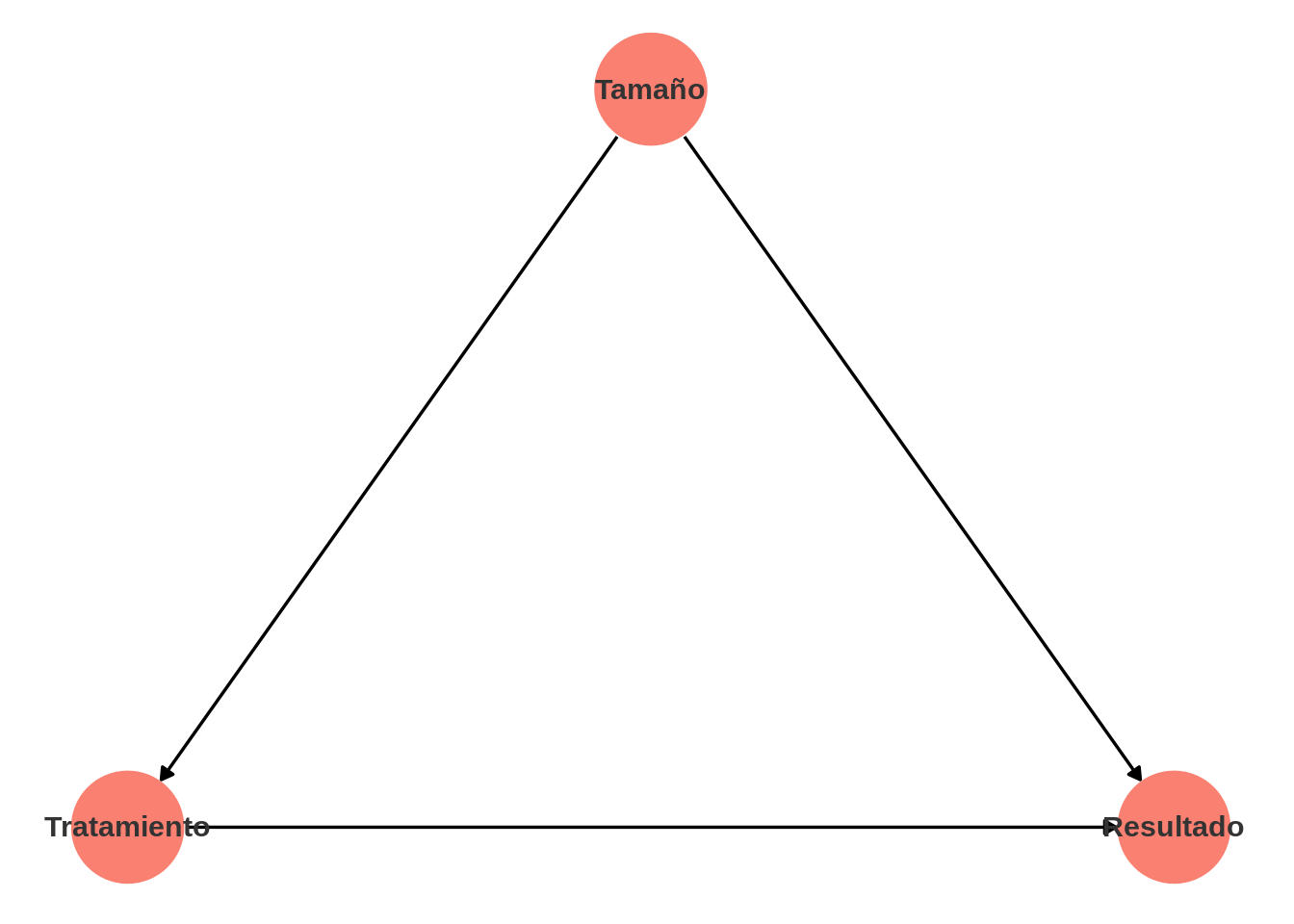

El tamaño de los cálculos afecta al resultado y a la asignación del tratamiento. Es un confusor si queremos entender el efecto del tratamiento en el resultado.
Partimos los datos según este confusor para “comparar peras con peras”.

Sin embargo, en el segundo ejemplo tenemos:

Código

library(dagitty)
library(ggdag)
dag_1 <- dagitty('dag{"Tratamiento" [exposure,pos="-3,0"]
  "Resultado" [outcome,pos="3,0"]
  "Presión" [pos="0,1"]
  "Tratamiento"  -> "Presión"
    "Presión" -> "Resultado"
    "Tratamiento" -> "Resultado"
  }')
dag_1_tidy <- tidy_dagitty(dag_1) 
dag_1_tidy |>
  ggplot(aes(x = x, y = y, xend = xend, yend = yend )) + 
  geom_dag_edges() +
  geom_dag_point(colour = "salmon", size = 20) +
  geom_dag_text(colour = "gray20") +
  theme_dag()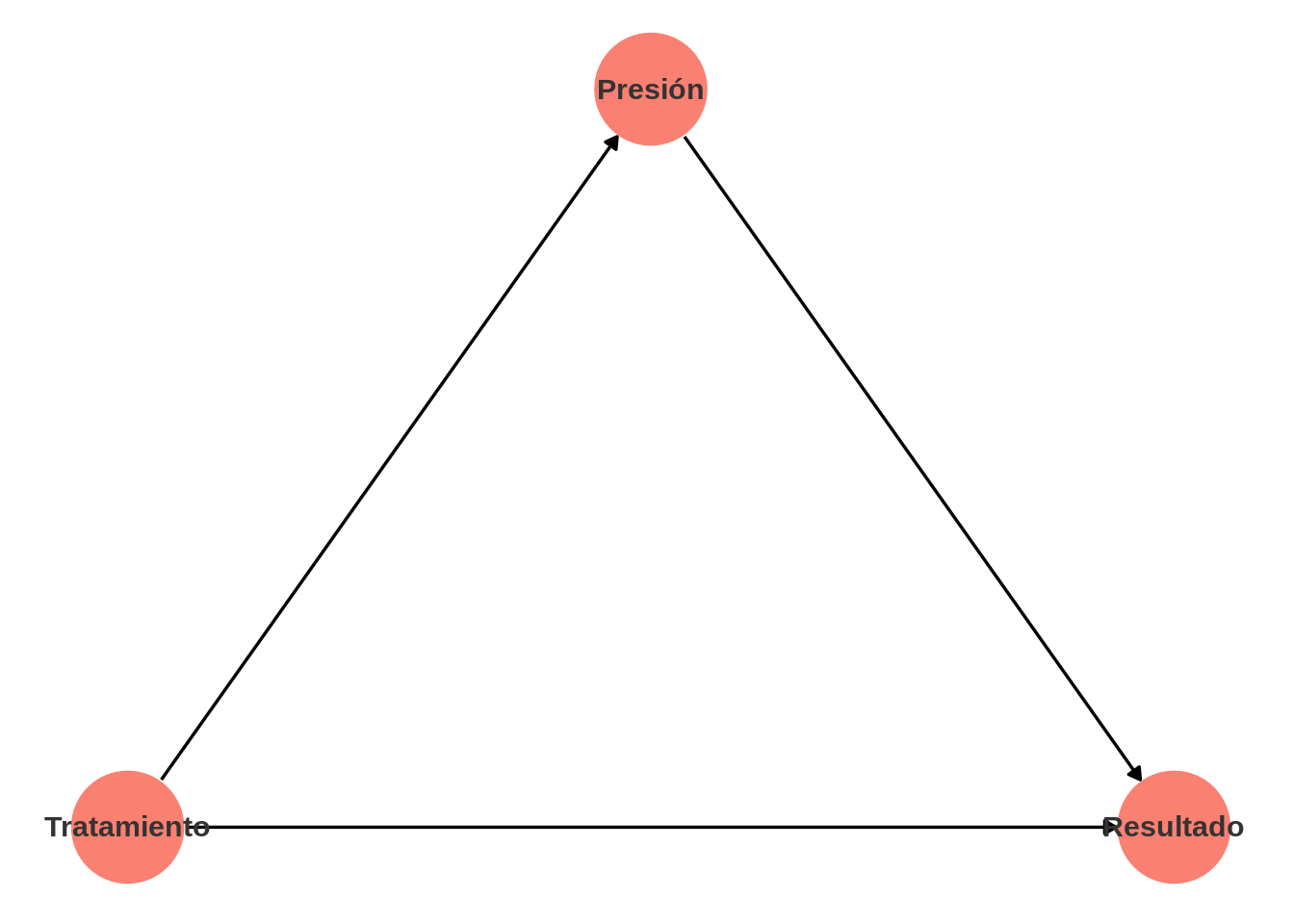

En este caso, la presión es consecuencia también del tratamiento, así que es un camino por medio del cual el tratamiento produce resultados.
Comparar el tratamiento dentro de grupos de presión alta o baja estima el efecto del tratamiento que no tiene qué ver con la regulación de la presión, lo cual da una respuesta incompleta.

Adicionalmente, en ambos ejemplos, estamos suponiendo que no existen otras variables confusoras que puedan afectar nuestro análisis. Qué tan correcta es esa suposición depende de que conozcamos los detalles de cómo fueron recopilados estos datos.

Ejemplo: prevalencia de anemia

En un estudio de hospitales en Australia se registró que 57% de una muestra pacientes tenían anemia cuando fueron ingresados. ¿Qué podemos decir acerca de la prevalencia de anemia en la población general de Australia? Con información básica acerca del proceso generador de esta muestra podemos concluir que será difícil generalizar con estos datos a la población general. La razón es que:

Muchas enfermedades graves (por ejemplo del corazón) pueden producir anemia.
Estas enfermededes hacen más probable que alguien sea hospitalizado.
Por lo tanto, en este estudio hay una asociación entre tener anemia y ser seleccionado para el estudio (tener anemia sube la probabilidad de ser seleccionado para el estudio)
Nuestra conclusión es que el 57% es probablemente una sobreestimación de la prevalencia de anemia en la población.

Código

dag_1 <- dagitty('dag{"Selección" [exposure, pos = "2,1"]
  "Anemia" [outcome, pos = "-1, 2.5"]
  "Hospitalización" [pos="1,2"]
  "Enfermedad" [pos="0, 3"]
  "Hospitalización" -> "Selección"
    "Enfermedad" -> "Anemia"
    "Anemia" -> "Hospitalización"
    "Enfermedad" -> "Hospitalización"
  }')
dag_1_tidy <- tidy_dagitty(dag_1) 
dag_1_tidy |>
  ggplot(aes(x = x, y = y, xend = xend, yend = yend )) + 
  geom_dag_edges() +
  geom_dag_point(colour = "salmon", size = 20) +
  geom_dag_text(colour = "gray20") +
  theme_dag()

Este diagrama indica que puede ser difícil generalizar con las personas que han sido seleccionadas, porque tanto la selección como la variable de interés tienen una causa común: la existencia o no de una enfermedad en la persona. Será difícil generalizar para las personas no observadas en el estudio.

Ejemplo: colisionadores y sesgo de selección

En los ejemplos anteriores vimos dos estructuras causales importantes para entender cómo interpretar datos: vimos variables confusoras que afectan a tratamiento y resultado (como el ejemplo de anemia), y vimos cadenas (como en el ejemplo de presión alta).

Una tercera estructura importante es la de colisionador: una variable que tiene como causa tratamiento y resultado. La interpretación de los datos cambia dependiendo si están condicionados a un valor del colisionador o no. Por ejemplo:

Supongamos que queremos entender la relación en desempeño en matemáticas y en español para estudiantes que entran a una universidad.
Encontramos una relación negativa entre las calificaciones de los dos exámenes: parece ser que habilidad verbal se contrapone a habilidad numérica.

¿Por qué tenemos que tener cuidado al interpretar esta correlación? ¿Existe esta correlación en la población general?

Código

library(dagitty)
library(ggdag)
dag_1 <- dagitty('dag{"Español" [exposure,pos="1,1"]
  "Mate" [outcome,pos="1,-1"]
  "Admisión" [pos="2,0"]
  "Español"  -> "Admisión"
    "Mate" -> "Admisión"
  }')
dag_1_tidy <- tidy_dagitty(dag_1) 
dag_1_tidy |>
  ggplot(aes(x = x, y = y, xend = xend, yend = yend )) + 
  geom_dag_edges() +
  geom_dag_point(colour = "salmon", size = 20) +
  geom_dag_text(colour = "gray20") +
  theme_dag()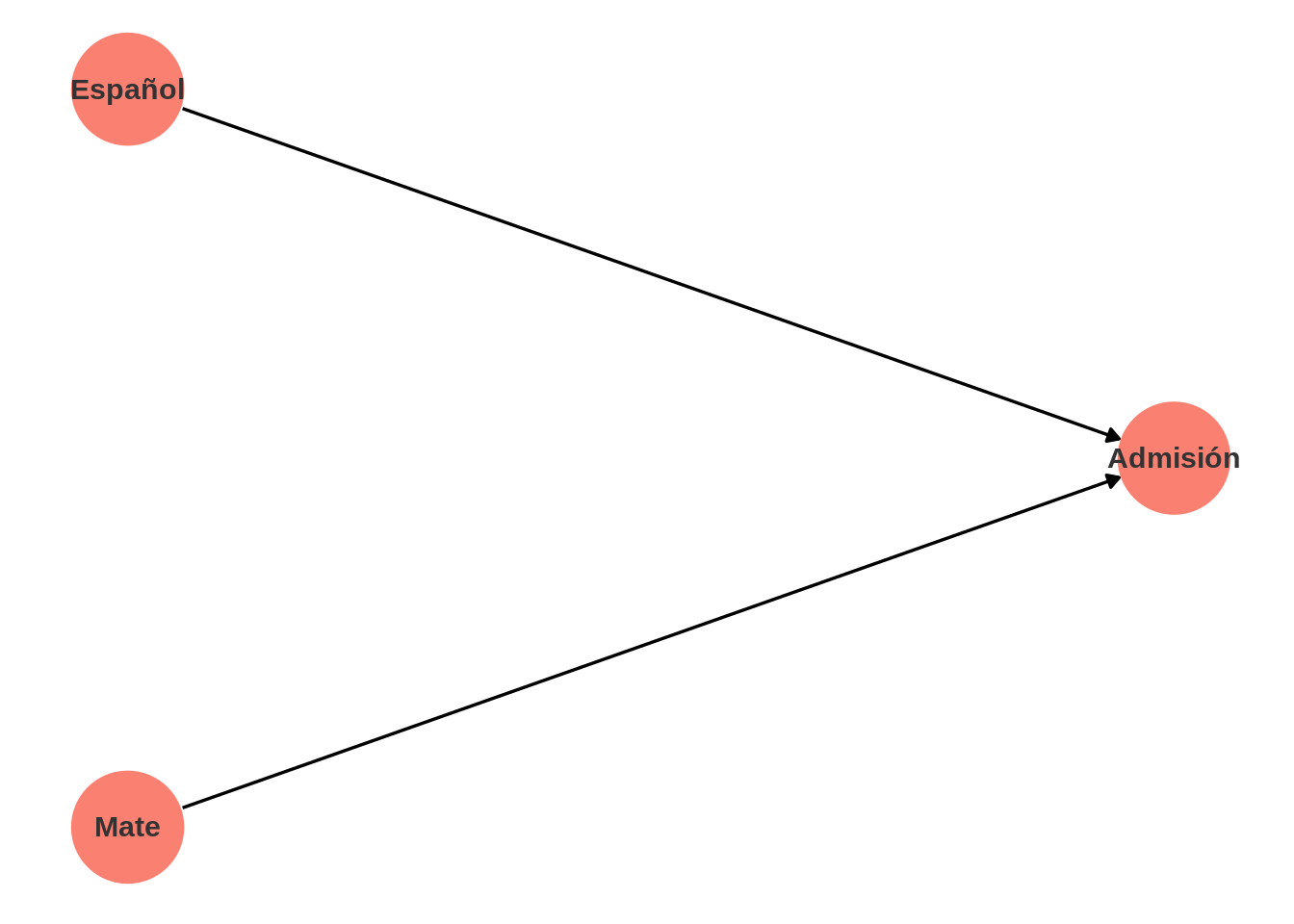

Descubrimos que la universidad hace una calificación compuesta de español y matemáticas para que los alumnos sean aceptados en la universidad
Esto quiere decir que para entrar es necesario al menos desempeñarse bien en alguna de las dos

Ahora observamos que aunque en la población general no hay tal relación, al seleccionar sólo a los alumnos de la universidad “activamos” una correlación debido al proceso de selección:

Código

set.seed(823)
tibble(x = rnorm(2000), y = rnorm(2000)) |> 
  mutate(aceptados = x + y > 1.5 ) |> 
ggplot(aes(x, y, colour = aceptados)) +
  geom_point(alpha = 0.5) +
  geom_smooth(method = "lm", se = FALSE)

`geom_smooth()` using formula 'y ~ x'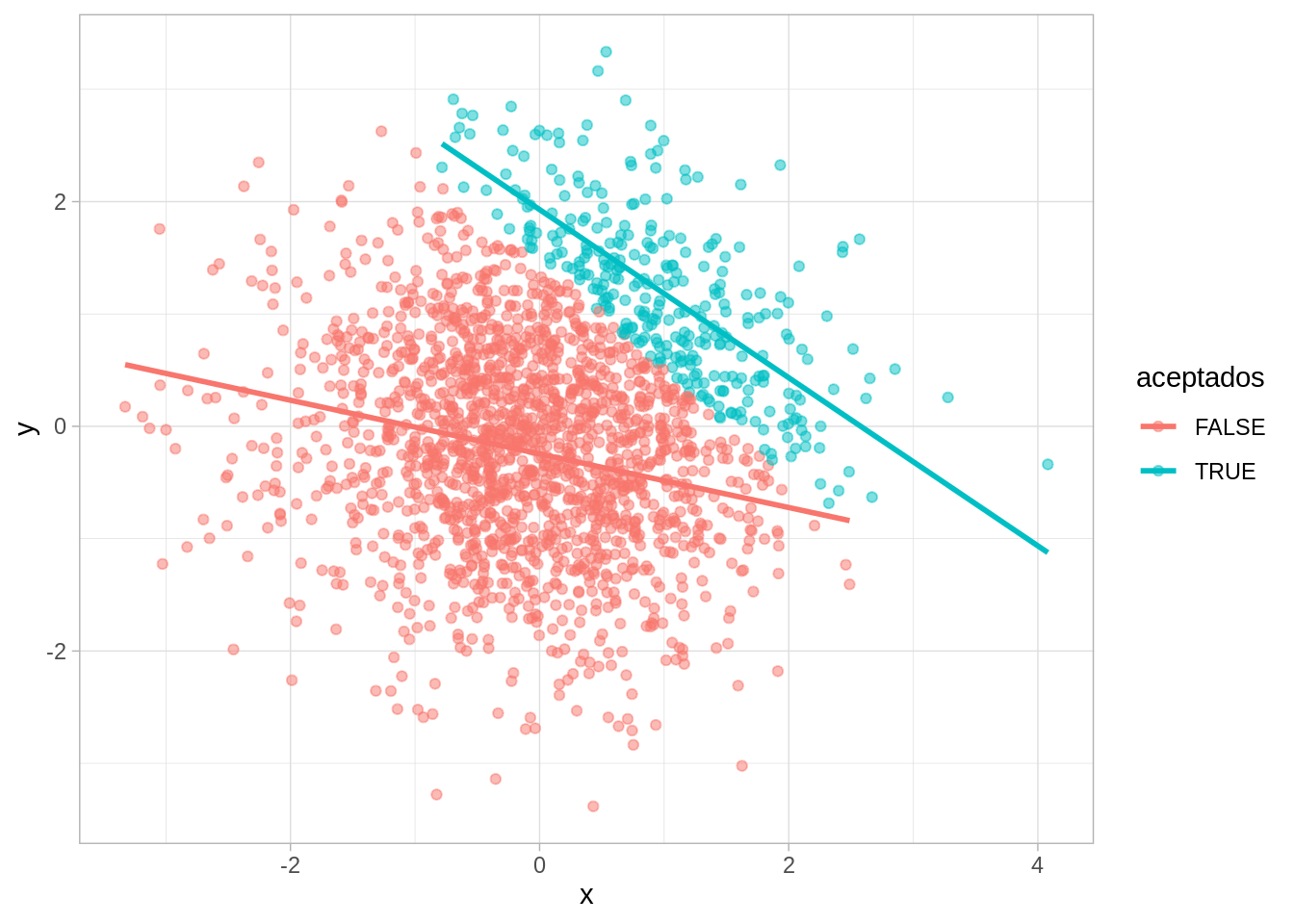

Ejemplo: sesgo de Berkson

Algunos estudios fueron publicados en la primera mitad de 2020 que notaban que el porcentaje fumadores entre los casos positivos de COVID era menor que en la población general, y se hicieron algunas interpretaciones acerca de este hecho. Estos estudios se hicieron con personas que se hicieron una prueba.

En este ejemplo replicaremos cómo es que podemos encontrar esta asociación en este tipo de estudios aún cuando no exista tal asociación en la población general (ver este artículo). Usaremos datos sintéticos (simulados).

Primero vamos a razonar acerca del proceso generador de datos y a hacer algunos supuestos:

En primer lugar, ¿cuándo decide hacerse alguien una prueba? A principios de 2020, son principalmente personas que tienen síntomas considerables, y trabajadores de salud (tengan o no síntomas).
Ser trabajador de salud incrementa el riesgo de contagiarse.
En algunos países, fumar está asociado con ser trabajador de salud (no tienen la misma tasa de tabaquismo que la población general).
Sólo observamos a las personas que se hicieron una prueba.

Podemos resumir cualitativamente con el siguiente diagrama:

Código

library(dagitty)
library(ggdag)
dag_1 <- dagitty('dag{"Covid" [outcome, pos = "-0.5, 2.5"]
  "Prueba" [pos="0,-2"]
  "TrabSalud" [pos="0, 3"]
  "Sintomas" [pos="-1, 1"]
  "Fumar" [pos = "1, 1"]
  "TrabSalud" -> "Covid"
  "TrabSalud" -> "Prueba"
  "TrabSalud" -> "Fumar"
  "Covid" -> "Sintomas"
  "Sintomas" -> "Prueba"
  }')
dag_1_tidy <- tidy_dagitty(dag_1) 
dag_1_tidy |>
  ggplot(aes(x = x, y = y, xend = xend, yend = yend )) + 
  geom_dag_edges() +
  geom_dag_point(colour = "salmon", size = 20) +
  geom_dag_text(colour = "gray20") +
  theme_dag()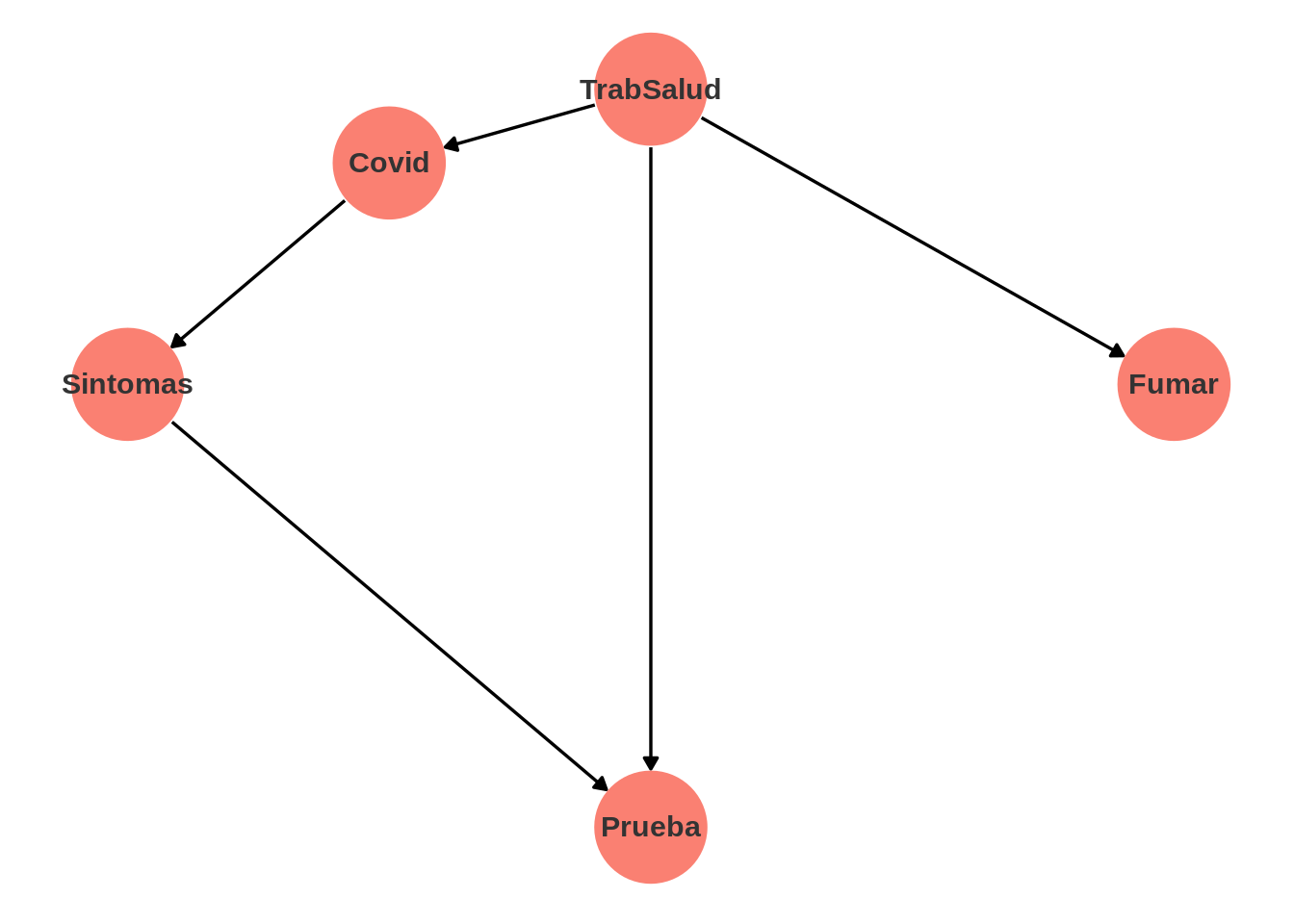

El código para simular es el siguiente: todas las variables toman valores 0 o 1, pero con diferentes probabilidades y dependiendo de las variables que son padres en la gráfica de arriba.

Simulamos 100,000 personas de las cuales aproximadamente el 1% son trabajadores de salud.
Suponemos que el 4% de los trabajadores de salud resultaron covid positivo y el 1% del resto de las personas resultaron covid positivo.
Suponemos que de las personas que tienen covid, el 50% tienen síntomas y de las personas que no tienen covid, el 1% tiene síntomas.
Suponemos que de los trabadores de salud el 99% se hicieron prueba (sin importar si tenían o no síntomas) y el resto de las personas se divide en 2, de los no trabadores de salud con síntomas, el 60% se hicieron una prueba y de los no trabajdores de salud sin síntomas, el 1% se hizo una prueba
De los trabajadores de salud, el 30% fuman, del resto de las personas el 10% fuman.

Código

set.seed(821)
#simular población
n <- 1000000
trab_salud <- rbinom(n, 1, 0.01)
covid <- rbinom(n, 1, ifelse(trab_salud==1, 0.04, 0.01))
datos <- tibble(trab_salud = trab_salud, covid) |> 
  mutate(sintomas = rbernoulli(n, ifelse(covid == 1, 0.5, 0.01))) |> 
  mutate(prueba = rbernoulli(n, ifelse(trab_salud ==1, 0.99, 0.6 * sintomas + 0.01))) |> 
  mutate(fumar = rbernoulli(n, ifelse(trab_salud == 1, 0.3, 0.1))) |> 
  mutate(covid = ifelse(covid ==1, "positivo", "negativo")) |> 
  mutate(fumar = ifelse(fumar, "fuma", "no_fuma"))

Suponemos ahora que tomamos como muestra a todas aquellas personas que se hicieron una prueba. En primer lugar, la proporción de fumadores en la muestra es un poco más alta que la población, porque los trabajadores de salud están sobrerrepresentados

Código

datos_pruebas <- filter(datos, prueba == 1)
table(datos_pruebas$fumar) |> prop.table()


     fuma   no_fuma 
0.1712317 0.8287683

Y ahora vemos que están asociados fumar y salir positivo:

Código

table(datos_pruebas$covid, datos_pruebas$fumar) |> prop.table(margin = 2) |> 
  round(2)

          
           fuma no_fuma
  negativo 0.91    0.87
  positivo 0.09    0.13

En la población no existe tal asociación, además de que la tasa de positivos es considerablemente más baja:

Código

table(datos$covid, datos$fumar) |> prop.table(margin = 2) |> 
  round(3)

          
            fuma no_fuma
  negativo 0.989   0.990
  positivo 0.011   0.010

En este ejemplo, al seleccionar sólo aquellas personas que tomaron una prueba, cambia la relación entre tener covid y ser trabajador de salud, pues sólo los que tienen síntomas de la población general toman la prueba. Esto produce que una prueba negativa esté más relacionada con ser trabajador de salud, y por lo tanto, mayor probabilidad de ser fumador.
También puede entenderse pensando que cuando tomamos solamente las personas que se hicieron pruebas, entonces los trabajadores de salud están sobrerrepresantados en la muestra.

Pearl, J., M. Glymour, y N. P. Jewell. 2016. Causal Inference in Statistics: A Primer. Wiley. https://books.google.com.mx/books?id=L3G-CgAAQBAJ.