12  Básicos de probabilidad y simulación

En esta parte comenzaremos a tratar el concepto de probabilidad de ocurrencia de eventos acerca de los que tenemos incertidumbre. Veremos que:

12.1 Definición de probabilidad

Una medida de probabilidad \(P\) es una función que asigna un número entre 0 y 1 a un evento \(E\) que puede o no ocurrir, y que satisface los siguientes axiomas:

  • (Evento seguro) \(P(\Omega) = 1\), donde \(\Omega\) es el evento que ocurre con certeza
  • (Aditividad) Si \(E\) y \(F\) son eventos tales que no pueden ocurrir simultáneamente, entonces el evento \(E\cup F\) que denota “al menos uno de los eventos \(E\) o \(F\) ocurre” satisface

\[P(E\cup F) = P(E) + P(F)\]

Nota: técnicamente, la aditividad debe cumplirse para cualquier colección numerable de eventos disjuntos.

Es decir, la probabilidad asigna números entre 0 y uno a eventos, de forma aditiva y tal que el evento seguro tiene probabilidad 1.

12.2 Probabilidad y frecuencias relativas

Aunque la probabilidad puede interpretarse como grados de creencia en la ocurrencia de un evento, es necesario que exista una conexión entre modelos de probabilidad y la ocurrencia de los eventos reales que nos interesa modelar. Esta conexión está dada como sigue:

Si tenemos un experimento aleatorio (por ejemplo, tirar un dado), y lo repetimos muchas veces de manera independiente, entonces las frecuencias relativas de ocurrencia de los eventos aproxima a las probabilidades teóricas.

Por ejemplo, si tiramos muchos volados con una moneda bien balanceada, al evento \(E\) = “tiramos sol” le asignamos \(P(E)=1/2\) según nuestro modelo. Entonces esperamos obtener alrededor de 1/2 de soles y 1/2 de águilas si tiramos una sucesión grande de volados.

Probabilidades y frecuencias

Supongamos que repetimos una gran cantidad \(n\) de veces un experimento, y que registramos \(k_n\) = cuántas veces ocurre un evento \(A\). La probabilidad de que ocurra \(A\) es

\[\lim_{n\to\infty} \frac{k_n}{n} \to P(A), \]

es decir, \(P(A)\) el la frecuencia al largo plazo de ocurrencia de \(A\).

Aunque podríamos hacer algunos experimentos físicos más reales, para este curso podemos hacer simulaciones de computadora del experimento que nos interesa.

Ejemplo: simulación de un dado

Consideremos modelar la tirada de un dado de 6 lados. En este caso, los eventos de interés son valores que puede tomar la tirada, por ejemplo, “Tirar un 6”, “tirar un número impar”, etc. Si en nuestro modelo consideramos que todos los lados tienen la misma probabilidad, podemos entonces definir

\[P(E_i) = 1/6,\]

para cada lado \(i=1,2,3,4,5,6\). A partir de estos valores podemos calcular la probabilidad de cualquier evento, por ejemplo, \(P(\textrm{tirar impar}) = 1/6 + 1/6 + 1/6 = 1/2\).

Podemos simular una tirada de dado como:

Código 
simular_dado <- function(caras = 1:6){
   sample(caras, 1)
}
simular_dado()
[1] 2

Ahora simulamos una gran cantidad de tiradas de dado:

Código 
set.seed(199652)
n <- 10000
sims_dado <- map_df(1:n, ~ c(n_sim = .x, resultado = simular_dado()))
head(sims_dado) 
# A tibble: 6 × 2
  n_sim resultado
  <int>     <int>
1     1         5
2     2         2
3     3         2
4     4         4
5     5         4
6     6         6

Esta es una variable numérica, pero como toma valores enteros del uno al seis, podemos resumir con frecuencias, como si fuera categórica:

Código 
sims_dado %>% 
   count(resultado) %>% 
   mutate(frec_relativa = n / sum(n))
# A tibble: 6 × 3
  resultado     n frec_relativa
      <int> <int>         <dbl>
1         1  1628         0.163
2         2  1711         0.171
3         3  1681         0.168
4         4  1680         0.168
5         5  1701         0.170
6         6  1599         0.160

Y nuestro modelo teórico (resultados equiprobables) coincide razonablemente bien con las frecuencias observadas a largo plazo. Podemos ver cómo convergen las frecuencias relativas por ejemplo del resultado 1:

Código 
sims_dado %>% 
   mutate(no_unos = cumsum(resultado == 1)) %>% 
   mutate(frec_uno = no_unos / n_sim) %>%
   filter(n_sim < 10000) %>% 
ggplot(aes(x = n_sim, y = frec_uno)) +
   geom_hline(yintercept = 1/6, colour = "red") +
   geom_line() + ylab("Frecuencia relativa de unos")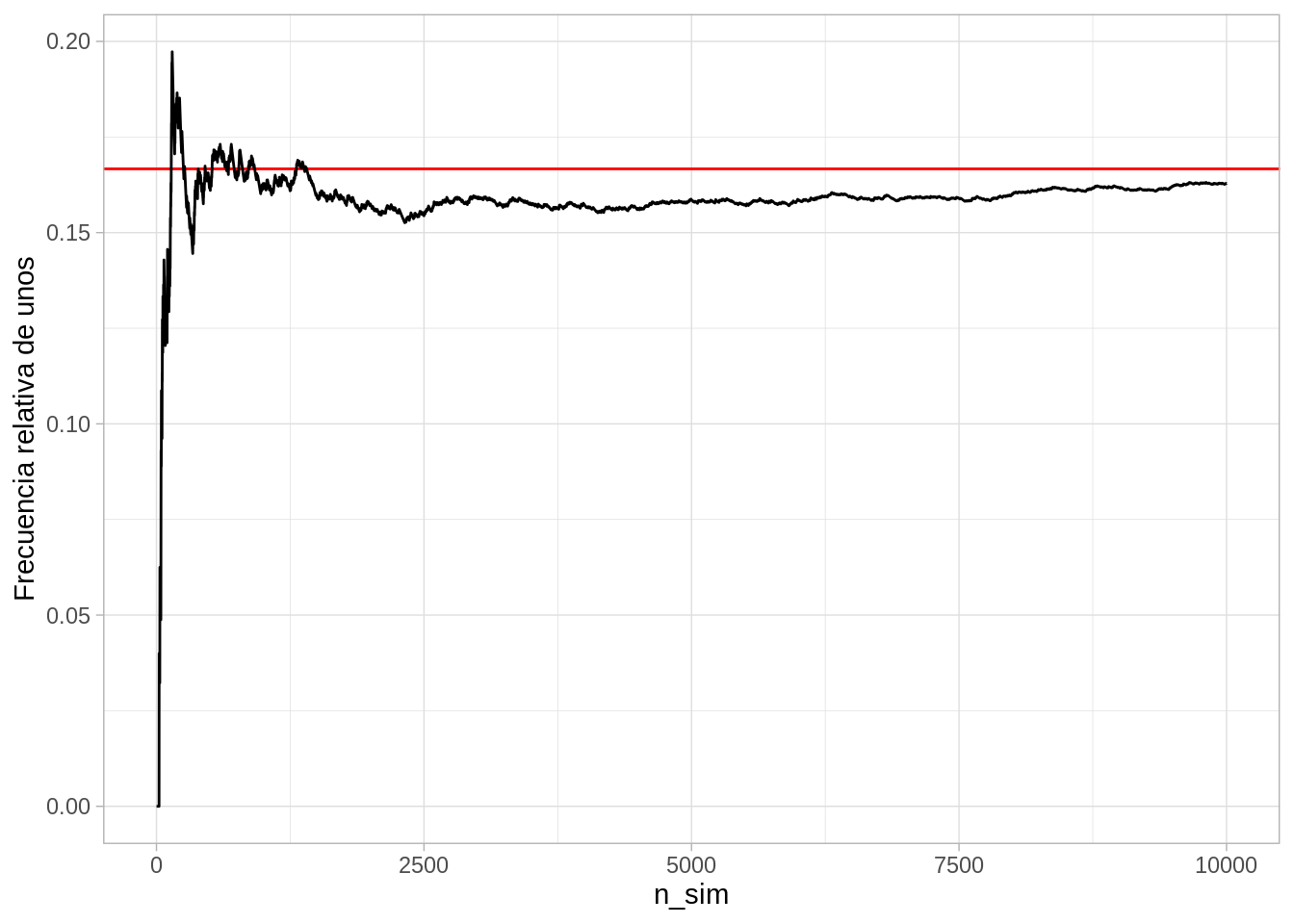

Nótese que cuando hay pocas repeticiones podemos ver fluctuaciones considerablemente grandes de la frecuencia relativa observada de unos. Sin embargo, conforme aumentamos el tamaño de la muesstra observada, esas fluctuaciones son más chicas.

12.3 Datos y modelos de probabilidad

¿Cómo podemos usar modelos de probablidad para describir datos observados? La idea (simplificada) es la siguiente:

  • Hacemos una hipótesis acerca de cómo es el modelo de probabilidad asociado a un fenómeno.
  • Observamos una muestra de datos del fenómeno que nos interesa.
  • Evaluamos si las fluctuaciones observadas debidas a la información limitada que tenemos (una muestra) son consistentes con el modelo de probabilidad.

Consideremos el ejemplo de los dados. Supongamos que lanzamos el dado un número no muy grande de veces, de manera independendiente y observamos:

Código 
frecs_obs <- tibble(resultado = 1:6,
                    n = c(5, 7, 5, 10, 8, 5)) |> 
   mutate(frec = n / sum(n))
frecs_obs |>  kable(digits = 2)
resultado n frec
1 5 0.12
2 7 0.17
3 5 0.12
4 10 0.25
5 8 0.20
6 5 0.12

Nos preguntamos si este resultado podría ser observado bajo los supuestos de nuestro modelo de probabilidad, que en este caso, es el de resultados equiprobables, es decir 1/6 para cada cara. Podemos por ejemplo graficar los datos junto con simulaciones del modelo, en búsqueda de desajustes:

Código 
set.seed(8834)
# una vez
sim_exp <- map_df(1:40, ~ c(id = .x, resultado = simular_dado()))
# 19 veces
sims_exp <- map_df(1:19, function(x){
         sims <- map_df(1:40, ~ c(id = .x, resultado = simular_dado()) )
         sims$rep <- x
         sims
         })
Código 
frec_sims <- sims_exp |> 
   group_by(rep, resultado) |>   
   summarise(n = n()) |> 
   mutate(frec = n / sum(n))
`summarise()` has grouped output by 'rep'. You can override using the `.groups`
argument.
Código 
obs_sims_tbl <- bind_rows(frec_sims, frecs_obs |>  mutate(rep = 20))
ggplot(obs_sims_tbl, aes(x = resultado, y = frec)) +
   geom_col() +
   facet_wrap(~rep)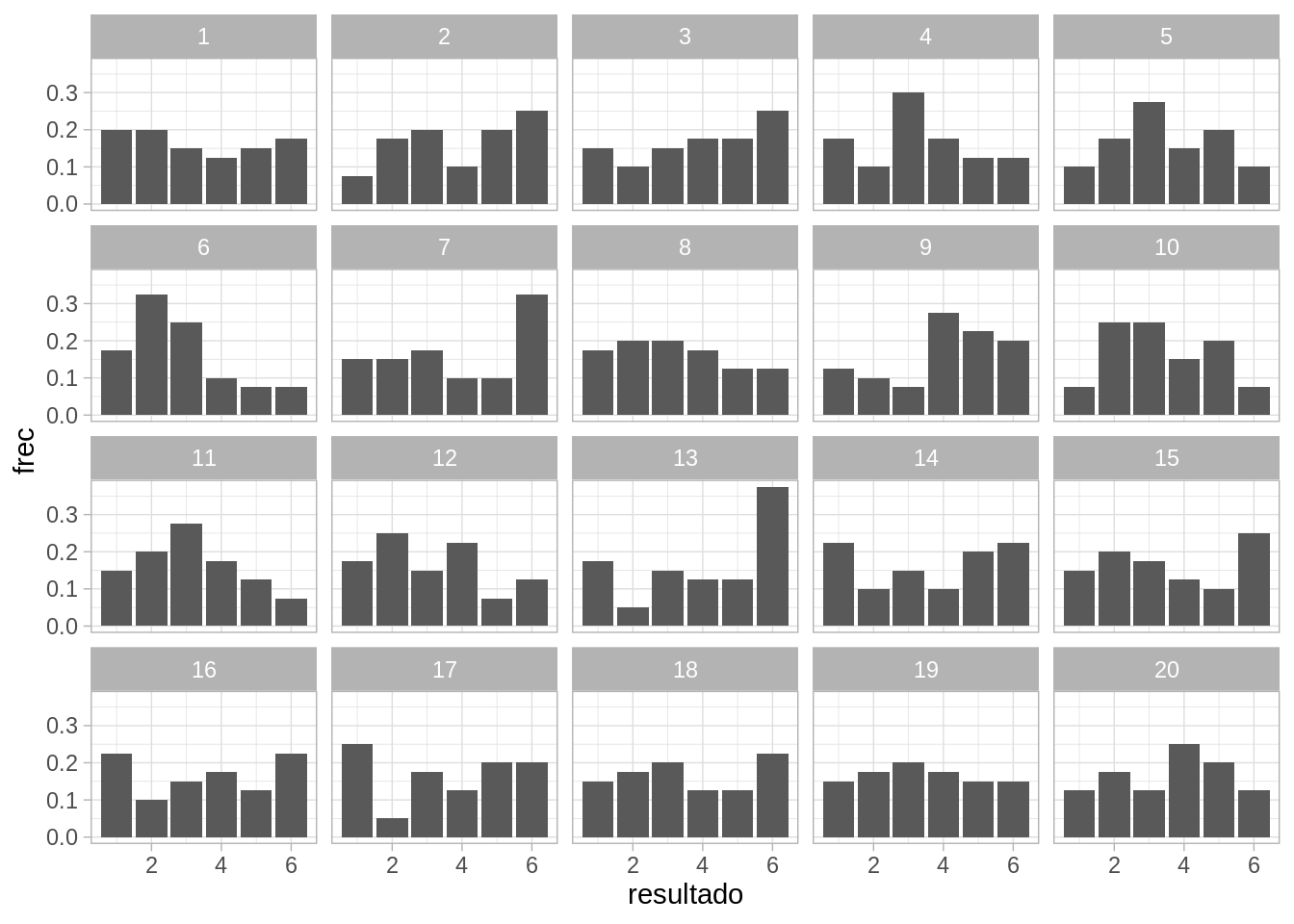

En este caso, no vemos ninguna característica de los datos observados que no sea consistente las fluctuaciones esperadas para un tamaño de muestra de \(n=40\).

Observación: como veremos, muchas veces proponemos modelos que tienen parámetros que deben ser estimados con la muestra. Este caso más común y, lo más simple es tener una muestra para estimar los parámetros, y después evaluar el ajuste con una nueva muestra de prueba. Si sólo tenemos una muestra para ajustar parámetros y ajustar, entonces debemos ser más cuidadosos en la evaluación.

12.4 Simulación y modelos

Una vez que tenemos un modelo apropiado para los datos de interés, tenemos métodos analíticos que podemos utilizar para calcular propiedades de nuestro modelo aleatorio. Por ejemplo, el valor esperado de una tirada de dado se puede definir analíticamente, pero también podemos definirla como la media de una gran cantidad de tiradas de dado independientes.

Métodos Monte Carlo

Los métodos Monte Carlo son métodos que utilizan simulación de un modelo probabilístico para calcular cantidades asociadas al modelo.

Ejemplo: simulando dos dados

Para dos dados, del modelo que consideraremos consiste en denotar cada tirada como \((x,y)\). Cada dado se tira de forma separada, y todos los resultados \((x,y)\) tienen la misma probabilidad igual a 1/36. Definimos entonces:

Código 
sim_dados <- function(num_dados = 2, num_caras = 6){
   resultado <- sample(1:num_caras, num_dados, replace = TRUE)
   names(resultado) <- paste0("dado_", 1:num_dados)
   resultado
}
sim_dados()
dado_1 dado_2 
     5      3

Ahora simulamos un número grande de veces el experimento:

Código 
set.seed(2323)
sims <- map_df(1:50000, ~ sim_dados())
sims
# A tibble: 50,000 × 2
   dado_1 dado_2
    <int>  <int>
 1      5      6
 2      3      3
 3      2      5
 4      3      5
 5      6      4
 6      2      2
 7      3      6
 8      6      5
 9      3      4
10      1      1
# … with 49,990 more rows

Ahora que tenemos estas simulaciones, podemos estimar por ejemplo el valor esperado de la suma de dos tiradas de dados, o también el rango intercuartiles.

Código 
sims_media <- 
   sims |>  
   mutate(suma = dado_1 + dado_2) |>  
   summarise(media = mean(suma), cuartil_inf = quantile(suma, 0.25), cuartil_sup = quantile(suma, 0.75)) 
sims_media 
# A tibble: 1 × 3
  media cuartil_inf cuartil_sup
  <dbl>       <dbl>       <dbl>
1  7.00           5           9

Y podemos calcular otras cantidades que puedes ser de interés, por ejemplo, ¿ cuál es la probabilidad de tirar más de nueve con dos dados?. Primero calculamos en qué simulaciones ocurre \(E\):

Código 
sims_e <- 
   sims |>  
   mutate(suma = dado_1 + dado_2) |> 
   mutate(evento_E = (suma > 9)) 
sims_e
# A tibble: 50,000 × 4
   dado_1 dado_2  suma evento_E
    <int>  <int> <int> <lgl>   
 1      5      6    11 TRUE    
 2      3      3     6 FALSE   
 3      2      5     7 FALSE   
 4      3      5     8 FALSE   
 5      6      4    10 TRUE    
 6      2      2     4 FALSE   
 7      3      6     9 FALSE   
 8      6      5    11 TRUE    
 9      3      4     7 FALSE   
10      1      1     2 FALSE   
# … with 49,990 more rows

Y ahora calculamos la frecuencia relativa de ocurrencia de \(E\)

Código 
sims_e |> 
   summarise(frec_e = mean(evento_E))
# A tibble: 1 × 1
  frec_e
   <dbl>
1  0.166

Puedes confirmar el resultado que obtuvimos arriba usando la aditividad de la probabilidad